Eine Einführung in den Merge-Sortierungsalgorithmus
Merge-Sort ist ein Sortieralgorithmus, der auf der "Divide and Conquer"-Technik basiert. Es ist einer der effizientesten Sortieralgorithmen.
In diesem Artikel erfahren Sie mehr über die Funktionsweise des Merge-Sort-Algorithmus, den Algorithmus des Merge-Sorts, seine zeitliche und räumliche Komplexität und seine Implementierung in verschiedenen Programmiersprachen wie C++, Python und JavaScript.
Wie funktioniert der Merge-Sort-Algorithmus?
Merge-Sort funktioniert nach dem Prinzip des Teilens und Herrschens. Merge-Sort zerlegt ein Array wiederholt in zwei gleiche Unterarrays, bis jedes Unterarray aus einem einzigen Element besteht. Schließlich werden alle diese Unterarrays so zusammengeführt, dass das resultierende Array sortiert wird.
Dieses Konzept lässt sich anhand eines Beispiels effizienter erklären. Betrachten Sie ein unsortiertes Array mit den folgenden Elementen: {16, 12, 15, 13, 19, 17, 11, 18}.
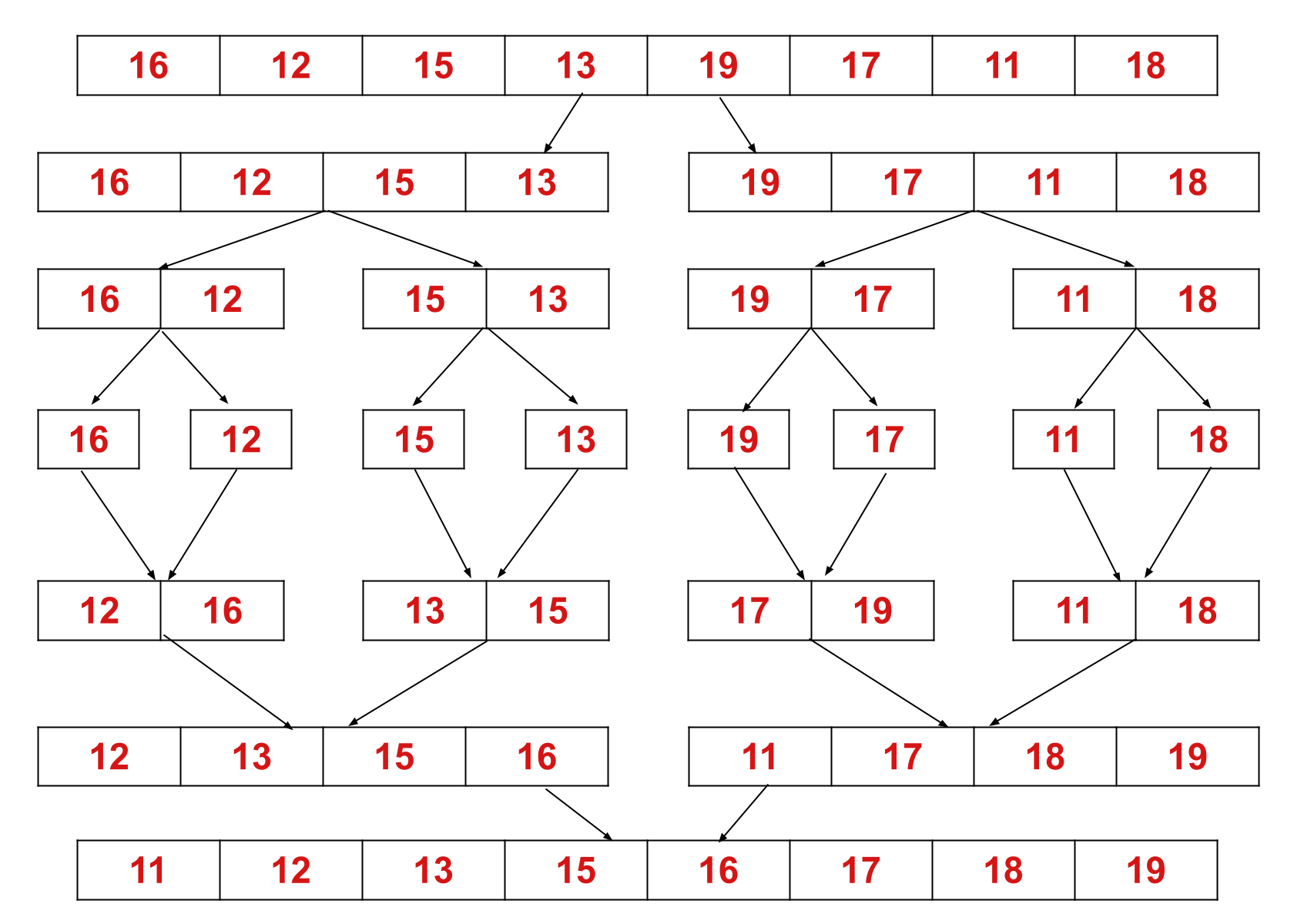
Hier teilt der Merge-Sort-Algorithmus das Array in zwei Hälften, ruft sich selbst für die beiden Hälften auf und führt dann die beiden sortierten Hälften zusammen.
Sortieralgorithmus zusammenführen
Unten ist der Algorithmus der Zusammenführungssortierung:
MergeSort(arr[], leftIndex, rightIndex)
if leftIndex >= rightIndex
return
else
Find the middle index that divides the array into two halves:
middleIndex = leftIndex + (rightIndex-leftIndex)/2
Call mergeSort() for the first half:
Call mergeSort(arr, leftIndex, middleIndex)
Call mergeSort() for the second half:
Call mergeSort(arr, middleIndex+1, rightIndex)
Merge the two halves sorted in step 2 and 3:
Call merge(arr, leftIndex, middleIndex, rightIndex)
Zeit- und Raumkomplexität des Merge-Sort-Algorithmus
Der Merge-Sortieralgorithmus kann in Form der folgenden Wiederholungsbeziehung ausgedrückt werden:
T(n) = 2T(n/2) + O(n)
Nachdem Sie diese Rekursionsbeziehung mit dem Master-Theorem oder der Rekursionsbaummethode gelöst haben, erhalten Sie die Lösung als O(n logn). Somit beträgt die Zeitkomplexität des Zusammenführungssortieralgorithmus O(n logn) .
Die Zeitkomplexität der Merge-Sortierung im günstigsten Fall: O(n logn)
Die durchschnittliche Zeitkomplexität der Zusammenführungssortierung: O(n logn)
Die Worst-Case-Zeitkomplexität der Merge-Sortierung: O(n logn)
Die Hilfsraumkomplexität des Mischsortieralgorithmus ist O(n), da n Hilfsraum in der Mischsortierimplementierung benötigt wird.
C++-Implementierung des Merge-Sort-Algorithmus
Unten ist die C++-Implementierung des Merge-Sort-Algorithmus:
// C++ implementation of the
// merge sort algorithm
#include <iostream>
using namespace std;
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
void merge(int arr[], int leftIndex, int middleIndex, int rightIndex)
{
int leftSubarraySize = middleIndex - leftIndex + 1;
int rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
int L[leftSubarraySize], R[rightSubarraySize];
// Copying data to temporary arrays L[] and R[]
for (int i = 0; i < leftSubarraySize; i++)
L[i] = arr[leftIndex + i];
for (int j = 0; j < rightSubarraySize; j++)
R[j] = arr[middleIndex + 1 + j];
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
int i = 0;
// Initial index of Right subarray
int j = 0;
// Initial index of merged subarray
int k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
void mergeSort(int arr[], int leftIndex, int rightIndex)
{
if(leftIndex >= rightIndex)
{
return;
}
int middleIndex = leftIndex + (rightIndex - leftIndex)/2;
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 16, 12, 15, 13, 19, 17, 11, 18 };
int size = sizeof(arr) / sizeof(arr[0]);
cout << "Unsorted array:" << endl;
printArray(arr, size);
mergeSort(arr, 0, size - 1);
cout << "Sorted array:" << endl;
printArray(arr, size);
return 0;
}Ausgabe:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19JavaScript-Implementierung des Merge-Sort-Algorithmus
Unten sehen Sie die JavaScript-Implementierung des Merge-Sort-Algorithmus:
// JavaScript implementation of the
// merge sort algorithm
// This function merges two subarrays of arr[]
// Left subarray: arr[leftIndex..middleIndex]
// Right subarray: arr[middleIndex+1..rightIndex]
function merge(arr, leftIndex, middleIndex, rightIndex) {
let leftSubarraySize = middleIndex - leftIndex + 1;
let rightSubarraySize = rightIndex - middleIndex;
// Create temporary arrays
var L = new Array(leftSubarraySize);
var R = new Array(rightSubarraySize);
// Copying data to temporary arrays L[] and R[]
for(let i = 0; i<leftSubarraySize; i++) {
L[i] = arr[leftIndex + i];
}
for (let j = 0; j<rightSubarraySize; j++) {
R[j] = arr[middleIndex + 1 + j];
}
// Merge the temporary arrays back into arr[leftIndex..rightIndex]
// Initial index of Left subarray
var i = 0;
// Initial index of Right subarray
var j = 0;
// Initial index of merged subarray
var k = leftIndex;
while (i < leftSubarraySize && j < rightSubarraySize)
{
if (L[i] <= R[j])
{
arr[k] = L[i];
i++;
}
else
{
arr[k] = R[j];
j++;
}
k++;
}
// If there're some remaining elements in L[]
// Copy to arr[]
while (i < leftSubarraySize)
{
arr[k] = L[i];
i++;
k++;
}
// If there're some remaining elements in R[]
// Copy to arr[]
while (j < rightSubarraySize)
{
arr[k] = R[j];
j++;
k++;
}
}
function mergeSort(arr, leftIndex, rightIndex) {
if(leftIndex >= rightIndex) {
return
}
var middleIndex = leftIndex + parseInt((rightIndex - leftIndex)/2);
mergeSort(arr, leftIndex, middleIndex);
mergeSort(arr, middleIndex+1, rightIndex);
merge(arr, leftIndex, middleIndex, rightIndex);
}
// Function to print the elements
// of the array
function printArray(arr, size) {
for(let i = 0; i<size; i++) {
document.write(arr[i] + " ");
}
document.write("<br>");
}
// Driver code:
var arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ];
var size = arr.length;
document.write("Unsorted array:<br>");
printArray(arr, size);
mergeSort(arr, 0, size - 1);
document.write("Sorted array:<br>");
printArray(arr, size);Ausgabe:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19
Python-Implementierung des Merge-Sort-Algorithmus
Unten ist die Python-Implementierung des Merge-Sort-Algorithmus:
# Python implementation of the
# merge sort algorithm
def mergeSort(arr):
if len(arr) > 1:
# Finding the middle index of the array
middleIndex = len(arr)//2
# Left half of the array
L = arr[:middleIndex]
# Right half of the array
R = arr[middleIndex:]
# Sorting the first half of the array
mergeSort(L)
# Sorting the second half of the array
mergeSort(R)
# Initial index of Left subarray
i = 0
# Initial index of Right subarray
j = 0
# Initial index of merged subarray
k = 0
# Copy data to temp arrays L[] and R[]
while i < len(L) and j < len(R):
if L[i] < R[j]:
arr[k] = L[i]
i = i + 1
else:
arr[k] = R[j]
j = j + 1
k = k + 1
# Checking if there're some remaining elements
while i < len(L):
arr[k] = L[i]
i = i + 1
k = k + 1
while j < len(R):
arr[k] = R[j]
j = j + 1
k = k + 1
# Function to print the elements
# of the array
def printArray(arr, size):
for i in range(size):
print(arr[i], end=" ")
print()
# Driver code
arr = [ 16, 12, 15, 13, 19, 17, 11, 18 ]
size = len(arr)
print("Unsorted array:")
printArray(arr, size)
mergeSort(arr)
print("Sorted array:")
printArray(arr, size)
Ausgabe:
Unsorted array:
16 12 15 13 19 17 11 18
Sorted array:
11 12 13 15 16 17 18 19Andere Sortieralgorithmen verstehen
Sortieren ist einer der am häufigsten verwendeten Algorithmen in der Programmierung. Sie können Elemente in verschiedenen Programmiersprachen mit verschiedenen Sortieralgorithmen wie Quick-Sort, Bubble-Sort, Merge-Sort, Insert-Sort usw. sortieren.
Bubble-Sort ist die beste Wahl, wenn Sie den einfachsten Sortieralgorithmus kennenlernen möchten.
