7 Algorithmen, die jeder Programmierer kennen sollte
Als Programmierstudent haben Sie im Laufe Ihrer Karriere wahrscheinlich viele verschiedene Algorithmen kennengelernt. Die Beherrschung verschiedener Algorithmen ist für jeden Programmierer unerlässlich.
Bei so vielen Algorithmen kann es schwierig sein, den Überblick über das Wesentliche zu behalten. Wenn Sie sich auf ein Vorstellungsgespräch vorbereiten oder einfach nur Ihre Fähigkeiten auffrischen, wird diese Liste es relativ einfach machen. Lesen Sie weiter, während wir die wichtigsten Algorithmen für Programmierer auflisten.
1. Dijkstras Algorithmus
Edsger Dijkstra war einer der einflussreichsten Informatiker seiner Zeit und trug zu vielen verschiedenen Bereichen der Informatik bei, darunter Betriebssysteme, Compilerbau und vieles mehr. Einer der bemerkenswertesten Beiträge von Dijkstra ist die Genialität seines Shortest Path Algorithmus für Graphen, auch bekannt als Dijkstra's Shortest Path Algorithm.
Der Algorithmus von Dijkstra findet den einzelnen kürzesten Weg in einem Graphen von einer Quelle zu allen Graphscheitelpunkten. Bei jeder Iteration des Algorithmus wird ein Scheitelpunkt mit dem minimalen Abstand von der Quelle hinzugefügt und einer, der im aktuellen kürzesten Pfad nicht existiert. Dies ist die gierige Eigenschaft, die vom Algorithmus von Djikstra verwendet wird.
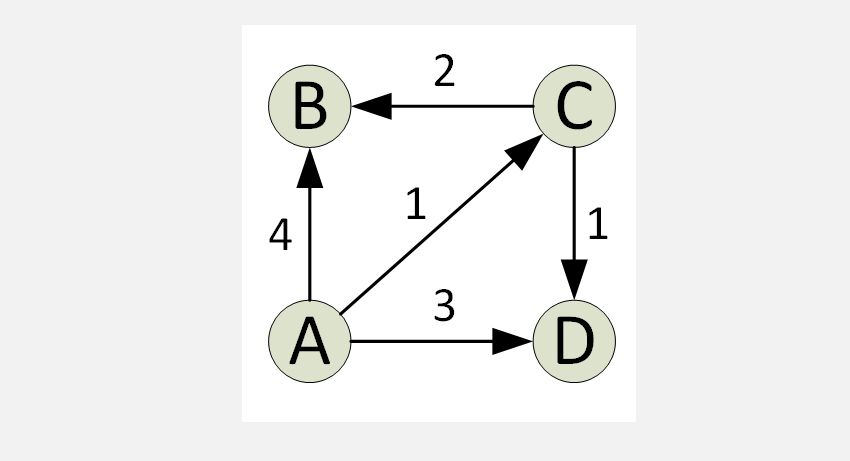
Der Algorithmus wird typischerweise unter Verwendung eines Satzes implementiert. Der Algorithmus von Dijkstra ist sehr effizient, wenn er mit einem Min Heap implementiert wird; Sie können den kürzesten Weg in nur O(V+ElogV) Zeit finden (V ist die Anzahl der Ecken und E ist die Anzahl der Kanten in einem gegebenen Graphen).
Der Algorithmus von Dijkstra hat seine Grenzen; es funktioniert nur bei gerichteten und ungerichteten Graphen mit Kanten mit positivem Gewicht. Für negative Gewichtungen ist der Bellman-Ford-Algorithmus typischerweise vorzuziehen.
Interviewfragen beinhalten häufig den Algorithmus von Djikstra, daher empfehlen wir dringend, seine komplizierten Details und Anwendungen zu verstehen.
2. Sortierung zusammenführen
Wir haben einige Sortieralgorithmen auf dieser Liste, und Mergesort ist einer der wichtigsten Algorithmen. Es handelt sich um einen effizienten Sortieralgorithmus, der auf der Programmiertechnik Divide and Conquer basiert. Im schlimmsten Fall kann Merge-Sort „n“ Zahlen in nur O(nlogn) Zeit sortieren. Im Vergleich zu primitiven Sortiertechniken wie Bubble Sort (die O(n^2) Zeit in Anspruch nehmen) ist die Merge-Sortierung hervorragend effizient.
Beim Merge-Sort wird das zu sortierende Array wiederholt in Subarrays zerlegt, bis jedes Subarray aus einer einzigen Zahl besteht. Der rekursive Algorithmus führt dann wiederholt die Unterarrays zusammen und sortiert das Array.
3. Schnellsortierung
Quicksort ist ein weiterer Sortieralgorithmus, der auf der Programmiertechnik Divide and Conquer basiert. Bei diesem Algorithmus wird zunächst ein Element als Pivot gewählt und dann das gesamte Array um diesen Pivot herum partitioniert.
Wie Sie wahrscheinlich schon vermutet haben, ist ein guter Pivot entscheidend für eine effiziente Sortierung. Der Pivot kann entweder ein zufälliges Element, das Medienelement, das erste Element oder sogar das letzte Element sein.
Quicksort-Implementierungen unterscheiden sich oft darin, wie sie einen Pivot auswählen. Im durchschnittlichen Fall sortiert Quicksort ein großes Array mit einem guten Pivot in nur O(nlogn) Zeit.
Der allgemeine Pseudocode von Quicksort partitioniert das Array wiederholt auf dem Pivot und positioniert es an der richtigen Position des Subarrays. Es platziert auch die Elemente, die kleiner als der Pivot sind, links davon und Elemente, die größer als der Pivot sind, rechts davon.
4. Tiefensuche
Die Tiefensuche (DFS) ist einer der ersten Graphalgorithmen, die Schülern gelehrt werden. DFS ist ein effizienter Algorithmus, der verwendet wird, um einen Graphen zu durchlaufen oder zu durchsuchen. Es kann auch modifiziert werden, um beim Durchqueren von Bäumen verwendet zu werden.
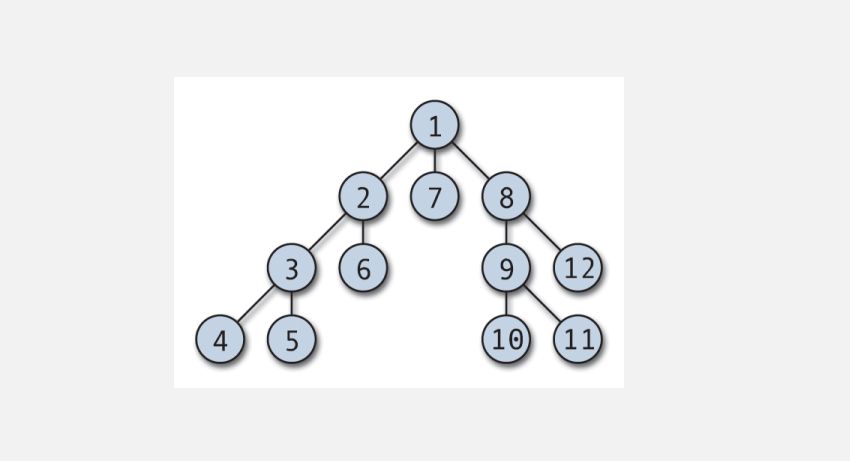
Die DFS-Traversierung kann von jedem beliebigen Knoten aus beginnen und taucht in jeden benachbarten Scheitelpunkt ein. Der Algorithmus wird zurückverfolgt, wenn es keinen unbesuchten Scheitelpunkt oder eine Sackgasse gibt. DFS wird normalerweise mit einem Stack und einem booleschen Array implementiert, um die besuchten Knoten zu verfolgen. DFS ist einfach zu implementieren und außergewöhnlich effizient; es funktioniert (V+E), wobei V die Anzahl der Ecken und E die Anzahl der Kanten ist.
Typische Anwendungen der DFS-Traversierung sind die topologische Sortierung, das Erkennen von Zyklen in einem Graphen, das Finden von Pfaden und das Auffinden stark verbundener Komponenten.
5. Breitenorientierte Suche
Breadth-First Search (BFS) wird auch als Level-Order-Traversal für Bäume bezeichnet. BFS arbeitet in O(V+E) ähnlich einem DFS-Algorithmus. BFS verwendet jedoch eine Warteschlange anstelle des Stapels. DFS taucht in den Graphen ein, während BFS den Graphen der Breite nach durchquert.
Der BFS-Algorithmus verwendet eine Warteschlange, um die Scheitelpunkte zu verfolgen. Nicht besuchte benachbarte Scheitelpunkte werden besucht, markiert und in die Warteschlange gestellt. Wenn der Scheitelpunkt keinen angrenzenden Scheitelpunkt hat, wird ein Scheitelpunkt aus der Warteschlange entfernt und untersucht.
BFS wird häufig in Peer-to-Peer-Netzwerken verwendet, dem kürzesten Pfad eines ungewichteten Graphen und um den minimalen Spannbaum zu finden.
6. Binäre Suche
Die binäre Suche ist ein einfacher Algorithmus, um das erforderliche Element in einem sortierten Array zu finden. Es funktioniert, indem es das Array wiederholt in zwei Hälften teilt. Ist das erforderliche Element kleiner als das mittlere Element, wird die linke Seite des mittleren Elements weiterverarbeitet; andernfalls wird die rechte Seite halbiert und erneut durchsucht. Der Vorgang wird wiederholt, bis das gewünschte Element gefunden ist.
Die Zeitkomplexität der binären Suche im ungünstigsten Fall ist O(logn), was sie beim Durchsuchen linearer Arrays sehr effizient macht.
7. Minimale Spanning-Tree-Algorithmen
Ein minimaler Spannbaum (MST) eines Graphen hat die minimalen Kosten unter allen möglichen Spannbäumen. Die Kosten eines Spannbaums hängen vom Gewicht seiner Kanten ab. Es ist wichtig zu beachten, dass es mehr als einen minimalen Spannbaum geben kann. Es gibt zwei Haupt-MST-Algorithmen, nämlich Kruskals und Prims.
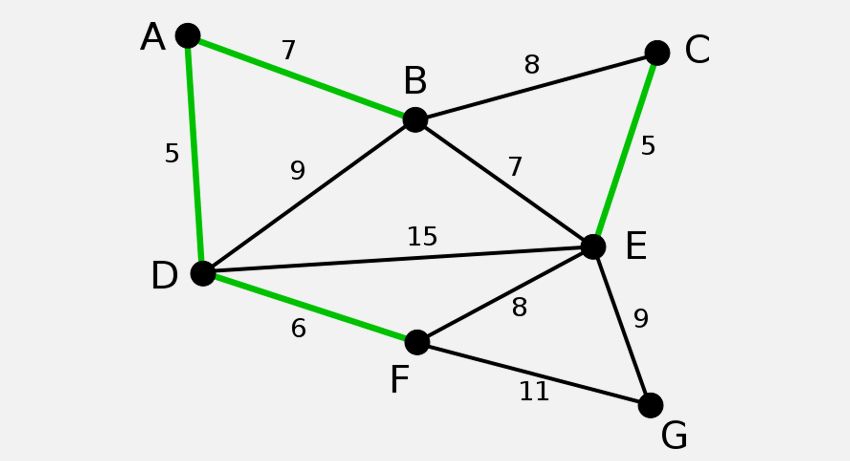
Der Algorithmus von Kruskal erzeugt den MST, indem er die Kante mit minimalen Kosten zu einer wachsenden Menge hinzufügt. Der Algorithmus sortiert zuerst Kanten nach ihrem Gewicht und fügt dann Kanten ausgehend vom Minimum zum MST hinzu.
Es ist wichtig zu beachten, dass der Algorithmus keine Kanten hinzufügt, die einen Kreis bilden. Der Algorithmus von Kruskal wird für dünn besetzte Graphen bevorzugt.
Der Algorithmus von Prim verwendet ebenfalls eine Greedy-Eigenschaft und ist ideal für dichte Graphen. Die zentrale Idee in Prims MST besteht darin, zwei verschiedene Sätze von Scheitelpunkten zu haben; ein Satz enthält die wachsende MST, während der andere nicht verwendete Scheitelpunkte enthält. Bei jeder Iteration wird die Kante mit minimalem Gewicht ausgewählt, die die beiden Sätze verbindet.
Minimale Spanning-Tree-Algorithmen sind für die Clusteranalyse, Taxonomie und Broadcast-Netzwerke unerlässlich.
Ein effizienter Programmierer beherrscht Algorithmen
Programmierer lernen und entwickeln ihre Fähigkeiten ständig weiter, und es gibt einige grundlegende Grundlagen, die jeder beherrschen muss. Ein erfahrener Programmierer kennt die verschiedenen Algorithmen, deren Vor- und Nachteile und welcher Algorithmus für ein bestimmtes Szenario am besten geeignet ist.
