Dynamische Programmierung: Beispiele, allgemeine Probleme und Lösungen

Eskere Guru

Es besteht kein Zweifel, dass dynamische Programmierprobleme in einem Coding-Interview sehr einschüchternd sein können. Selbst wenn Sie wissen, dass ein Problem mithilfe einer dynamischen Programmiermethode gelöst werden muss, ist es eine Herausforderung, in einem begrenzten Zeitraum eine funktionierende Lösung zu finden.

Der beste Weg, um bei dynamischen Programmierproblemen gut zu sein, besteht darin, so viele wie möglich durchzugehen. Sie müssen sich nicht unbedingt die Lösung für jedes Problem merken, aber es ist gut, eine Vorstellung davon zu haben, wie man eines implementiert.

Was ist dynamische Programmierung?

Einfach ausgedrückt ist die dynamische Programmierung eine Optimierungsmethode für rekursive Algorithmen, von denen die meisten zur Lösung von Rechen- oder mathematischen Problemen verwendet werden.

Sie können es auch als algorithmische Technik zur Lösung eines Optimierungsproblems bezeichnen, indem Sie es in einfachere Unterprobleme aufteilen. Ein Schlüsselprinzip, auf dem die dynamische Programmierung basiert, ist, dass die optimale Lösung eines Problems von den Lösungen seiner Unterprobleme abhängt.

Überall dort, wo wir eine rekursive Lösung sehen, bei der dieselben Eingaben wiederholt aufgerufen werden, können wir sie mithilfe dynamischer Programmierung optimieren. Die Idee ist, die Ergebnisse von Teilproblemen einfach zu speichern, damit wir sie bei Bedarf später nicht neu berechnen müssen.

Dynamisch programmierte Lösungen weisen eine Polynomkomplexität auf, die eine viel schnellere Laufzeit als andere Techniken wie Rekursion oder Backtracking gewährleistet. In den meisten Fällen reduziert die dynamische Programmierung die Zeitkomplexität, auch als Big-O bezeichnet , von exponentiell zu polynomiell.

Nachdem Sie eine gute Vorstellung davon haben, was dynamische Programmierung ist, ist es an der Zeit, einige häufig auftretende Probleme und deren Lösungen zu untersuchen.

Dynamische Programmierprobleme

1. Rucksackproblem

Problemstellung

Bestimmen Sie anhand einer Reihe von Elementen mit jeweils einem Gewicht und einem Wert die Anzahl der Elemente, die in eine Sammlung aufgenommen werden sollen, damit das Gesamtgewicht einen bestimmten Grenzwert nicht überschreitet und der Gesamtwert so groß wie möglich ist.

Sie erhalten zwei ganzzahlige Array- Werte [0..n-1] und Gewichte [0..n-1], die Werte und Gewichte darstellen, die n Elementen zugeordnet sind. Ebenfalls angegeben ist eine ganze Zahl W, die die Rucksackkapazität darstellt.

Hier lösen wir das 0/1-Rucksackproblem, was bedeutet, dass wir entweder einen Gegenstand hinzufügen oder ihn ausschließen können.

Algorithmus

  • Erstellen Sie ein zweidimensionales Array mit n + 1 Zeilen und w + 1 Spalten. Eine Zeilennummer n bezeichnet den Satz von Gegenständen von 1 bis i , und eine Spaltennummer w bezeichnet die maximale Tragfähigkeit des Beutels.
  • Der numerische Wert bei [i] [j] gibt den Gesamtwert der Gegenstände bis i in einer Tasche an, die ein maximales Gewicht von j tragen kann.
  • Wählen Sie an jeder Koordinate [i] [j] im Array den Maximalwert aus, den wir ohne Element i erhalten können , oder den Maximalwert, den wir mit Element i erhalten können – je nachdem, welcher Wert größer ist.
  • Der maximal erreichbare Wert durch Einbeziehung von Artikel i ist die Summe aus Artikel i selbst und dem Maximalwert, der mit der verbleibenden Kapazität des Rucksacks erzielt werden kann.
  • Führen Sie diesen Schritt aus, bis Sie den Maximalwert für die W- te Zeile gefunden haben.

Code

 def FindMax(W, n, values, weights):
 MaxVals = [[0 for x in range(W + 1)] for x in range(n + 1)]

 for i in range(n + 1):
 for w in range(W + 1):
 if i == 0 or w == 0:
 MaxVals[i][w] = 0
 elif weights[i-1] <= w:
 MaxVals[i][w] = max(values[i-1]
 + MaxVals[i-1][w-weights[i-1]],
 MaxVals[i-1][w])
 else:
 MaxVals[i][w] = MaxVals[i-1][w]

 return MaxVals[n][W]

2. Münzwechselproblem

Problemstellung

Angenommen, Sie erhalten eine Reihe von Zahlen, die die Werte jeder Münze darstellen. Finden Sie bei einem bestimmten Betrag die Mindestanzahl an Münzen, die für diesen Betrag erforderlich sind.

Dynamische Programmierung: Beispiele, allgemeine Probleme und Lösungen - coins

Algorithmus

  • Initialisieren Sie ein Array der Größe n + 1 , wobei n der Betrag ist. Initialisieren Sie den Wert jedes Index i im Array so, dass er dem Betrag entspricht. Dies gibt die maximale Anzahl von Münzen (unter Verwendung von Münzen mit dem Nennwert 1) an, die erforderlich sind, um diesen Betrag zu bilden.
  • Da es für 0 keine Bezeichnung gibt, initialisieren Sie den Basisfall mit dem Array [0] = 0 .
  • Für jeden anderen Index i vergleichen wir den Wert darin (der anfänglich auf n + 1 gesetzt ist ) mit dem Wertearray [ik] +1 , wobei k kleiner als i ist . Dies überprüft im Wesentlichen das gesamte Array bis i-1, um die minimal mögliche Anzahl von Münzen zu finden, die wir verwenden können.
  • Wenn der Wert in einem Array [ik] + 1 kleiner als der vorhandene Wert in Array [i] ist , ersetzen Sie den Wert in Array [i] durch den Wert in Array [ik] +1 .

Code

 def coin_change(d, amount, k):
 numbers = [0]*(amount+1)

 for j in range(1, amount+1):
 minimum = amount
 for i in range(1, k+1):
 if(j >= d[i]):
 minimum = min(minimum, 1 + numbers[jd[i]])
 numbers[j] = minimum

 return numbers[amount]

3. Fibonacci

Problemstellung

Die Fibonacci-Reihe ist eine Folge von ganzen Zahlen, wobei die nächste ganze Zahl in der Reihe die Summe der beiden vorherigen ist.

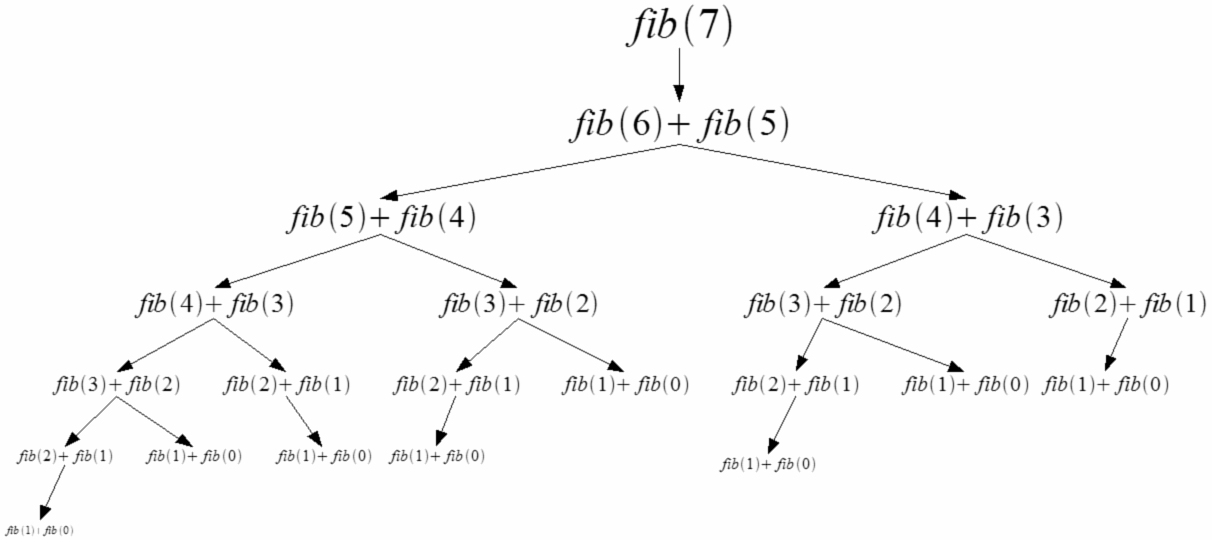
Es wird durch die folgende rekursive Beziehung definiert: F (0) = 0, F (n) = F (n-1) + F (n-2) , wobei F (n) der n- te Term ist. In diesem Problem müssen wir alle Zahlen in einer Fibonacci-Sequenz bis zu einem bestimmten n- ten Term generieren.

Dynamische Programmierung: Beispiele, allgemeine Probleme und Lösungen - FibbonacciRecurisive

Algorithmus

  • Verwenden Sie zunächst einen rekursiven Ansatz, um die angegebene Wiederholungsbeziehung zu implementieren.
  • Um dieses Problem rekursiv zu lösen, muss F (n) in F (n-1) + F (n-2) zerlegt und dann die Funktion mit F (n-1) und F (n + 2) als Parametern aufgerufen werden. Wir tun dies, bis die Basisfälle mit n = 0 oder n = 1 erreicht sind.
  • Jetzt verwenden wir eine Technik namens Memoization. Speichern Sie die Ergebnisse aller Funktionsaufrufe in einem Array. Dies stellt sicher, dass für jedes n F (n) nur einmal berechnet werden muss.
  • Für alle nachfolgenden Berechnungen kann sein Wert einfach in konstanter Zeit aus dem Array abgerufen werden.

Code

 def fibonacci(n):
 fibNums = [0, 1]
 for i in range(2, n+1):
 fibNums.append(fibNums[i-1] + fibNums[i-2])
 return fibNums[n]

4. Längste zunehmende Folge

Problemstellung

Ermitteln Sie die Länge der am längsten zunehmenden Teilsequenz innerhalb eines bestimmten Arrays. Die am längsten zunehmende Teilfolge ist eine Teilfolge innerhalb eines Arrays von Zahlen mit aufsteigender Reihenfolge. Die Zahlen innerhalb der Teilsequenz müssen eindeutig und in aufsteigender Reihenfolge sein.

Außerdem müssen die Elemente der Sequenz nicht aufeinanderfolgend sein.

Algorithmus

  • Beginnen Sie mit einem rekursiven Ansatz, bei dem Sie den Wert der am längsten ansteigenden Teilsequenz jedes möglichen Subarrays von Index Null bis Index i berechnen, wobei i kleiner oder gleich der Größe des Arrays ist.
  • Um diese Methode in eine dynamische umzuwandeln, erstellen Sie ein Array, in dem der Wert für jede Teilsequenz gespeichert wird. Initialisieren Sie alle Werte dieses Arrays auf 0.
  • Jeder Index i dieses Arrays entspricht der Länge der am längsten ansteigenden Teilsequenz für ein Subarray der Größe i .
  • Überprüfen Sie nun für jeden rekursiven Aufruf von findLIS (arr, n) den n- ten Index des Arrays. Wenn dieser Wert 0 ist, berechnen Sie den Wert mit der Methode im ersten Schritt und speichern Sie ihn im n- ten Index.
  • Geben Sie schließlich den Maximalwert aus dem Array zurück. Dies ist die Länge der am längsten ansteigenden Teilsequenz einer gegebenen Größe n .

Code

 def findLIS(myArray):
 n = len(myArray)
 lis = [0]*n

 for i in range (1 , n):
 for j in range(0 , i):
 if myArray[i] > myArray[j] and lis[i]< lis[j] + 1 :
 lis[i] = lis[j]+1

 maxVal= 0
 for i in range(n):
 maxVal = max(maxVal , lis[i])

 return maxVal

Lösungen für dynamische Programmierprobleme

Nachdem Sie einige der beliebtesten Probleme bei der dynamischen Programmierung durchlaufen haben, ist es an der Zeit, die Lösungen selbst zu implementieren. Wenn Sie nicht weiterkommen, können Sie jederzeit auf den Algorithmus-Abschnitt für jedes der oben genannten Probleme zurückgreifen.

Angesichts der heutigen Beliebtheit von Techniken wie Rekursion und dynamischer Programmierung schadet es nicht, einige beliebte Plattformen zu besuchen, auf denen Sie solche Konzepte erlernen und Ihre Codierungsfähigkeiten verbessern können . Während Sie möglicherweise nicht täglich auf diese Probleme stoßen, werden Sie sie sicherlich in einem technischen Interview antreffen.

Das Know-how für häufig auftretende Probleme zahlt sich natürlich aus, wenn Sie Ihr nächstes Interview führen. Öffnen Sie also Ihre Lieblings-IDE und legen Sie los!