So finden Sie die Transponierung einer Matrix in mehreren Sprachen

Die Transponierung einer Matrix wird durch Vertauschen der Zeilen und Spalten der ursprünglichen Matrix erhalten. In diesem Artikel erfahren Sie, wie Sie mit C++, Python, JavaScript und C die Transponierte einer quadratischen und rechteckigen Matrix ermitteln.

Problemstellung

Sie erhalten eine Matrixmatte [][] . Sie müssen die Transponierte der Matrix finden und drucken.

Beispiele:

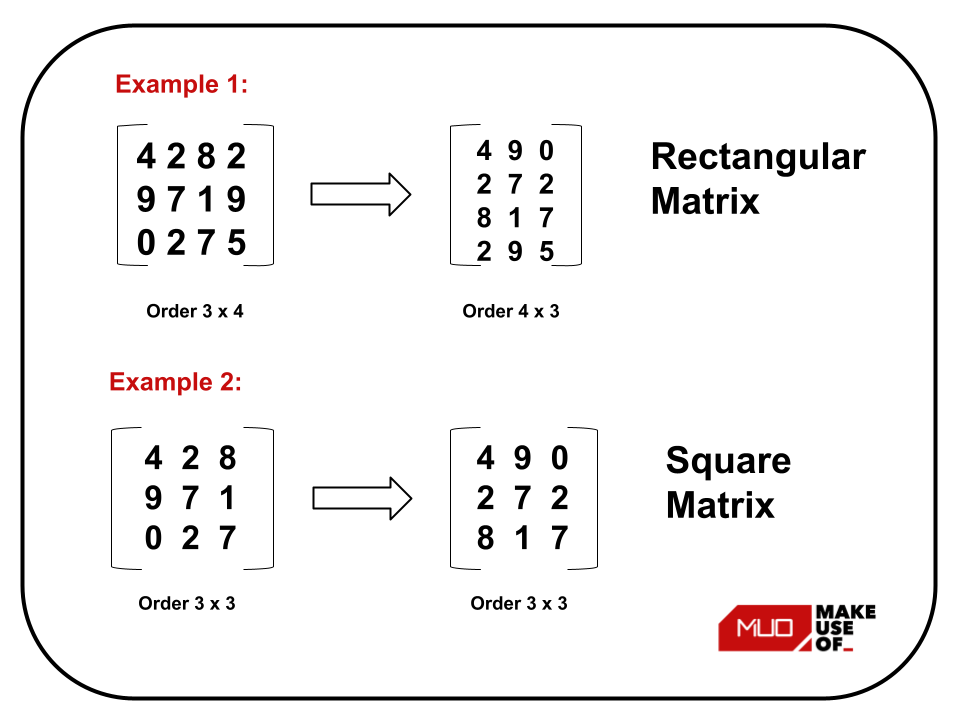
So finden Sie die Transponierte einer rechteckigen Matrix

1. Die Reihenfolge der Transponierung einer rechteckigen Matrix ist der der ursprünglichen Matrix entgegengesetzt. Wenn beispielsweise die Reihenfolge der ursprünglichen Matrix 3 x 4 beträgt, wäre die Reihenfolge der Transponierten dieser Matrix 4 x 3.
2. Speichern Sie jede Spalte der ursprünglichen Matrix als Zeilen in der transponierten Matrix, dh transposeMatrix[i][j] = mat[j][i].

C++-Programm zum Ermitteln der Transponierten einer rechteckigen Matrix

Unten ist das C++-Programm zum Ermitteln der Transponierten einer rechteckigen Matrix:

 // C++ program to find the transpose of a rectangular Matrix
 #include <iostream>
 using namespace std;
 // The order of the initial matrix is 3 x 4
 #define size1 3
 #define size2 4
 // Function to transpose a Matrix
 void transposeMatrix(int mat[][size2], int transposeMatrix[][size1])
 {
 for (int i=0; i<size2; i++)
 {
 for (int j=0; j<size1; j++)
 {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }
 // Driver Code
 int main()
 {
 int mat[size1][size2] = { {4, 2, 8, 2},
 {9, 7, 1, 9},
 {0, 2, 7, 5} };
 cout << "Initial Matrix:" << endl;
 // Printing the initial Matrix
 for (int i = 0; i < size1; i++)
 {
 for (int j = 0; j < size2; j++)
 {
 cout << mat[i][j] << " ";
 }
 cout << endl;
 }
 // Variable to store the transposed Matrix
 // The dimensions of transposedMatrix are opposite to that of mat
 int transposedMatrix[size2][size1];
 transposeMatrix(mat, transposedMatrix);
 cout << "Transposed Matrix:" << endl;
 // Printing the transposed Matrix
 for (int i = 0; i < size2; i++)
 {
 for (int j = 0; j < size1; j++)
 {
 cout << transposedMatrix[i][j] << " ";
 }
 cout << endl;
 }
 return 0;
 }

Ausgabe:

 Initial Matrix:
 4 2 8 2
 9 7 1 9
 0 2 7 5
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7
 2 9 5

Python-Programm zum Ermitteln der Transponierten einer rechteckigen Matrix

Unten ist das Python-Programm, um die Transponierte einer rechteckigen Matrix zu finden:

 # Python program to find the transpose of a rectangular Matrix
 # The order of the initial matrix is 3 x 4
 size1 = 3
 size2 = 4
 # Function to transpose a Matrix
 def transposeMatrix(mat, transposedMatrix):
 for i in range(size2):
 for j in range(size1):
 transposedMatrix[i][j] = mat[j][i]
 # Driver Code
 mat = [ [4, 2, 8, 2],
 [9, 7, 1, 9],
 [0, 2, 7, 5] ]
 print("Initial Matrix:")
 # Printing the initial Matrix
 for i in range(size1):
 for j in range(size2):
 print(mat[i][j], end=' ')
 print()
 # Variable to store the transposed Matrix
 # The dimensions of transposedMatrix are opposite to that of mat
 transposedMatrix = [[0 for x in range(size1)] for y in range(size2)]
 transposeMatrix(mat, transposedMatrix)
 print("Transposed Matrix:")
 # Printing the transposed Matrix
 for i in range(size2):
 for j in range(size1):
 print(transposedMatrix[i][j], end=' ')
 print()

Ausgabe:

 Initial Matrix:
 4 2 8 2
 9 7 1 9
 0 2 7 5
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7
 2 9 5

Verwandte: So finden Sie die LCM und GCD von zwei Zahlen in mehreren Sprachen

JavaScript-Programm zum Finden der Transponierten einer rechteckigen Matrix

Unten ist das JavaScript-Programm zum Ermitteln der Transponierten einer rechteckigen Matrix:

 // JavaScript program to find the transpose of a rectangular Matrix
 // The order of the initial matrix is 3 x 4
 var size1 = 3
 var size2 = 4
 // Function to transpose a Matrix
 function transposeMatrix(mat, transposeMatrix) {
 for (let i=0; i<size2; i++) {
 for (let j=0; j<size1; j++) {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }
 // Driver Code
 var mat = [ [4, 2, 8, 2],
 [9, 7, 1, 9],
 [0, 2, 7, 5] ];
 document.write("Initial Matrix:" + "<br>");
 // Printing the initial Matrix
 for (let i = 0; i < size1; i++) {
 for (let j = 0; j < size2; j++) {
 document.write(mat[i][j] + " ");
 }
 document.write("<br>");
 }
 // Variable to store the transposed Matrix
 // The dimensions of transposedMatrix are opposite to that of mat1
 var transposedMatrix = new Array(size2);
 for (let k = 0; k < size2; k++) {
 transposedMatrix[k] = new Array(size1);
 }
 transposeMatrix(mat, transposedMatrix);
 document.write("Transposed Matrix:" + "<br>");
 // Printing the transposed Matrix
 for (let i = 0; i < size2; i++) {
 for (let j = 0; j < size1; j++) {
 document.write(transposedMatrix[i][j] + " ");
 }
 document.write("<br>");
 }

Ausgabe:

 Initial Matrix:
 4 2 8 2
 9 7 1 9
 0 2 7 5
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7
 2 9 5

Verwandte: Wie man zwei Variablen in C++, Python und JavaScript vertauscht

C-Programm zum Ermitteln der Transponierten einer rechteckigen Matrix

Unten ist das C-Programm, um die Transponierte einer rechteckigen Matrix zu finden:

 // C program to find the transpose of a rectangular Matrix
 #include <stdio.h>
 // The order of the initial matrix is 3 x 4
 #define size1 3
 #define size2 4
 // Function to transpose a Matrix
 void transposeMatrix(int mat[][size2], int transposeMatrix[][size1])
 {
 for (int i=0; i<size2; i++)
 {
 for (int j=0; j<size1; j++)
 {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }
 // Driver Code
 int main()
 {
 int mat[size1][size2] = { {4, 2, 8, 2},
 {9, 7, 1, 9},
 {0, 2, 7, 5} };
 printf("Initial Matrix: ⁠n");
 // Printing the initial Matrix
 for (int i = 0; i < size1; i++)
 {
 for (int j = 0; j < size2; j++)
 {
 printf("%d ", mat[i][j]);
 }
 printf("⁠n");
 }
 // Variable to store the transposed Matrix
 // The dimensions of transposedMatrix are opposite to that of mat1
 int transposedMatrix[size2][size1];
 transposeMatrix(mat, transposedMatrix);
 printf("Transposed Matrix: ⁠n");
 // Printing the transposed Matrix
 for (int i = 0; i < size2; i++)
 {
 for (int j = 0; j < size1; j++)
 {
 printf("%d ", transposedMatrix[i][j]);
 }
 printf("⁠n");
 }
 return 0;
 }

Ausgabe:

 Initial Matrix:
 4 2 8 2
 9 7 1 9
 0 2 7 5
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7
 2 9 5

So finden Sie die Transponierung einer quadratischen Matrix

1. Die Transponierungsreihenfolge einer quadratischen Matrix ist dieselbe wie die der ursprünglichen Matrix. Wenn die Reihenfolge der ursprünglichen Matrix beispielsweise 3 x 3 beträgt, wäre die Reihenfolge der Transponierten dieser Matrix immer noch 3 x 3. Deklarieren Sie also eine Matrix mit derselben Ordnung wie die der ursprünglichen Matrix.
2. Speichern Sie jede Spalte der ursprünglichen Matrix als Zeilen in der transponierten Matrix, dh transposeMatrix[i][j] = mat[j][i].

C++-Programm zum Ermitteln der Transponierten einer quadratischen Matrix

Unten ist das C++-Programm zum Ermitteln der Transponierten einer quadratischen Matrix:

 // C++ program to find the transpose of a square matrix
 #include <iostream>
 using namespace std;
 // The order of the matrix is 3 x 3
 #define size 3
 // Function to transpose a Matrix
 void transposeMatrix(int mat[][size], int transposeMatrix[][size])
 {
 for (int i=0; i<size; i++)
 {
 for (int j=0; j<size; j++)
 {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }

 int main()
 {
 int mat[size][size] = { {4, 2, 8},
 {9, 7, 1},
 {0, 2, 7} };
 cout << "Initial Matrix:" << endl;
 // Printing the initial Matrix
 for (int i = 0; i < size; i++)
 {
 for (int j = 0; j < size; j++)
 {
 cout << mat[i][j] << " ";
 }
 cout << endl;
 }
 // Variable to store the transposed Matrix
 int transposedMatrix[size][size];
 transposeMatrix(mat, transposedMatrix);
 cout << "Transposed Matrix:" << endl;
 // Printing the transposed Matrix
 for (int i = 0; i < size; i++)
 {
 for (int j = 0; j < size; j++)
 {
 cout << transposedMatrix[i][j] << " ";
 }
 cout << endl;
 }
 return 0;
 }

Ausgabe:

 Initial Matrix:
 4 2 8
 9 7 1
 0 2 7
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7

Python-Programm zum Ermitteln der Transponierung einer quadratischen Matrix

Unten ist das Python-Programm, um die Transponierte einer quadratischen Matrix zu finden:

 # Python program to find the transpose of a square Matrix
 # The order of the initial matrix is 3 x 3
 size = 3
 # Function to transpose a Matrix
 def transposeMatrix(mat, transposedMatrix):
 for i in range(size):
 for j in range(size):
 transposedMatrix[i][j] = mat[j][i]
 # Driver Code
 mat = [ [4, 2, 8],
 [9, 7, 1],
 [0, 2, 7] ]
 print("Initial Matrix:")
 # Printing the initial Matrix
 for i in range(size):
 for j in range(size):
 print(mat[i][j], end=' ')
 print()
 # Variable to store the transposed Matrix
 transposedMatrix = [[0 for x in range(size)] for y in range(size)]
 transposeMatrix(mat, transposedMatrix)
 print("Transposed Matrix:")
 # Printing the transposed Matrix
 for i in range(size):
 for j in range(size):
 print(transposedMatrix[i][j], end=' ')
 print()

Ausgabe:

 Initial Matrix:
 4 2 8
 9 7 1
 0 2 7
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7

Verwandte: So finden Sie die Summe natürlicher Zahlen mit Rekursion

JavaScript-Programm zum Ermitteln der Transponierung einer quadratischen Matrix

Unten ist das JavaScript-Programm zum Ermitteln der Transponierten einer quadratischen Matrix:

 // JavaScript program to find the transpose of a square Matrix
 // The order of the initial matrix is 3 x 3
 var size = 3
 // Function to transpose a Matrix
 function transposeMatrix(mat, transposeMatrix) {
 for (let i=0; i<size; i++) {
 for (let j=0; j<size; j++) {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }
 // Driver Code
 var mat = [ [4, 2, 8],
 [9, 7, 1],
 [0, 2, 7] ];
 document.write("Initial Matrix:" + "<br>");
 // Printing the initial Matrix
 for (let i = 0; i < size; i++) {
 for (let j = 0; j < size; j++) {
 document.write(mat[i][j] + " ");
 }
 document.write("<br>");
 }
 // Variable to store the transposed Matrix
 // The dimensions of transposedMatrix are opposite to that of mat1
 var transposedMatrix = new Array(size);
 for (let k = 0; k < size; k++) {
 transposedMatrix[k] = new Array(size);
 }
 transposeMatrix(mat, transposedMatrix);
 document.write("Transposed Matrix:" + "<br>");
 // Printing the transposed Matrix
 for (let i = 0; i < size; i++) {
 for (let j = 0; j < size; j++) {
 document.write(transposedMatrix[i][j] + " ");
 }
 document.write("<br>");
 }

Ausgabe:

 Initial Matrix:
 4 2 8
 9 7 1
 0 2 7
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7

C-Programm zum Ermitteln der Transponierung einer quadratischen Matrix

Unten ist das C-Programm, um die Transponierte einer quadratischen Matrix zu finden:

 // C program to find the transpose of a square Matrix
 #include <stdio.h>
 // The order of the initial matrix is 3 x 3
 #define size 3
 // Function to transpose a Matrix
 void transposeMatrix(int mat[][size], int transposeMatrix[][size])
 {
 for (int i=0; i<size; i++)
 {
 for (int j=0; j<size; j++)
 {
 transposeMatrix[i][j] = mat[j][i];
 }
 }
 }
 // Driver Code
 int main()
 {
 int mat[size][size] = { {4, 2, 8},
 {9, 7, 1},
 {0, 2, 7} };
 printf("Initial Matrix: ⁠n");
 // Printing the initial Matrix
 for (int i = 0; i < size; i++)
 {
 for (int j = 0; j < size; j++)
 {
 printf("%d ", mat[i][j]);
 }
 printf("⁠n");
 }
 // Variable to store the transposed Matrix
 int transposedMatrix[size][size];
 transposeMatrix(mat, transposedMatrix);
 printf("Transposed Matrix: ⁠n");
 // Printing the transposed Matrix
 for (int i = 0; i < size; i++)
 {
 for (int j = 0; j < size; j++)
 {
 printf("%d ", transposedMatrix[i][j]);
 }
 printf("⁠n");
 }
 return 0;
 }

Ausgabe:

 Initial Matrix:
 4 2 8
 9 7 1
 0 2 7
 Transposed Matrix:
 4 9 0
 2 7 2
 8 1 7

Lösen Sie grundlegende Programmierprobleme basierend auf Matrizen

Eine Matrix ist ein Raster zum Speichern oder Anzeigen von Daten in einem strukturierten Format. Matrizen werden in der Programmierung häufig verwendet, um verschiedene Operationen durchzuführen. Wenn Sie alle Grundlagen von Codierungsinterviews abdecken möchten, müssen Sie wissen, wie Sie grundlegende Operationen wie Addition, Subtraktion, Multiplikation und mehr auf Matrizen durchführen.